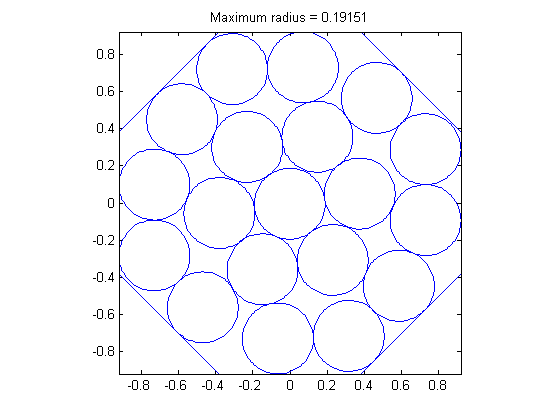
Packing Circles inside a Polygon

Given an N-sided polygon inscribed in the unit circle, and a set of M smaller circles of radius r. Find the maximum radius of the smaller circles that allows them all to fit inside the polygon without overlap.

N = 8;  % Number of sides on polygon
M = 19; % Number of circles to fit

toms r              % Radius of circles
x = tom('x', 2, M); % Coordinates of circle centers

clear pi % 3.1415...

theta = 2*pi/N;       % Angle covered by each side of the polygon

% Distance from the origin to the midpoint of the sides of the polygon
cdist = cos(theta/2);

% Create a set of equations that say that all circles are inside the
% polygon
phi = theta*(0:N-1)'; % Direction of the normal to the side of the polygon
polyEq = ( [cos(phi) sin(phi)]*x <= cdist-r );

% Create a set of equations that say that no circles overlap
circEq = cell(M-1,1);
for i=1:M-1
    circEq{i} = ( sqrt(sum((x(:,i+1:end)-repmat(x(:,i),1,M-i)).^2)) >= 2*r );
end

% Starting guess
x0 = { r == 0.5*sqrt(1/M), x == 0.3*randn(size(x)) };

% Solve the problem, maximizing r
options = struct;
% Try multiple starting guesses and choose best result
options.solver = 'multimin';
options.xInit = 30; % Number of different starting guesses
solution = ezsolve(-r,{polyEq,circEq},x0,options);

% Plot result
plot(cos(phi([1:end 1])+theta/2),sin(phi([1:end 1])+theta/2),'-') % Polygon
axis image
hold on
alpha = linspace(0,2*pi,100);
cx = solution.r*cos(alpha);
cy = solution.r*sin(alpha);
for i=1:M
    plot(solution.x(1,i)+cx,solution.x(2,i)+cy) % Circle number i
end
hold off
title(['Maximum radius = ' num2str(solution.r)]);

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Problem 1                      f_k      -0.191508243876529320
                                       sum(|constr|)      0.000000000000000222
                              f(x_k) + sum(|constr|)     -0.191508243876529090
                                              f(x_0)    974.949613401405490000

Solver: multiMin with local solver snopt.  EXIT=0.  INFORM=1.
Find local optima using multistart local search
Did 30 local tries. Found 30 local minima

FuncEv    1 ConstrEv   45 ConJacEv   45 Iter   22 MinorIter  215
CPU time: 21.953125 sec. Elapsed time: 22.672000 sec.