Circle Enclosing Points - SNOPT Example

TomSym implementation of GAMS Example (CIRCLE,SEQ=201)

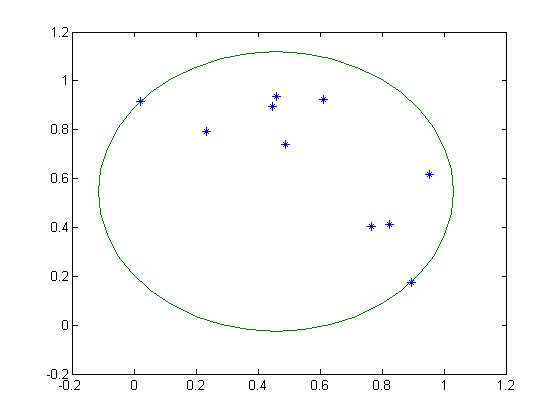
This is an example from the GAMS/SNOPT manual. Find the smallest circle that contains a number of given points.

Gill, P E, Murray, W, and Saunders, M A, GAMS/SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization, 1988.

% x coordinates (random data)
x = [0.950129285147175;0.231138513574288;0.606842583541787;...
     0.485982468709300;0.891298966148902;0.762096833027395;...
     0.456467665168341;0.018503643248224;0.821407164295253;...
     0.444703364353194];

% y coordinates (random data)
y = [0.615432348100095;0.791937037427035;0.921812970744803;...
     0.738207245810665;0.176266144494618;0.405706213062095;...
	 0.935469699107605;0.916904439913408;0.410270206990945;...
	 0.893649530913534];

% Variables
% a: x coordinate of center of circle
% b: y coordinate of center of circle
% r: radius
toms a b r

% Points must be inside circle and radius must be positive
eq1 = {r >= 0
    (x-a).^2 + (y-b).^2 <= r.^2};
obj = r;

% Parameters xmin,ymin,xmax,ymax;
xmin = min(x);
xmax = max(x);
ymin = min(y);
ymax = max(y);

% Set starting point
x0 = {a == (xmin+xmax)/2
    b == (ymin+ymax)/2
    r == sqrt( (a-xmin).^2 + (b-ymin).^2 )};

options = struct;
options.name = 'Inside circle';
solution = ezsolve(obj,eq1,x0,options);

a = solution.a;
b = solution.b;
r = solution.r;

figure(1);

th = 0:pi/20:2*pi;
x1 = r*cos(th)+a;
y1 = r*sin(th)+b;
plot(x,y,'*',x1,y1,'-');

Problem type appears to be: lpcon
===== * * * =================================================================== * * *
TOMLAB - Tomlab Optimization Inc. Development license  999001. Valid to 2010-02-05
=====================================================================================
Problem: ---  1: Inside circle                  f_k       0.572345341380648520
                                       sum(|constr|)      0.000000000558818603
                              f(x_k) + sum(|constr|)      0.572345341939467070
                                              f(x_0)      0.600898571720017370

Solver: snopt.  EXIT=0.  INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied

FuncEv    1 ConstrEv    7 ConJacEv    7 Iter    4 MinorIter    7
CPU time: 0.015625 sec. Elapsed time: 0.016000 sec.